Echantillonnage préférentiel (programmes 4 et 5)

Programme 4 On reprend le programme 3 dans le cas de l'absorption moyenne (évaluation de la fraction des photons absorbés avant d'atteindre les limites du carré). On modifie ce programme pour tenir compte du fait que les photons partent avec une fréquence uniformément distribuée sur un intervalle $[\nu_x,\nu_y]$ et que le coefficient d'absorption est dépendant de la fréquence. A chaque fréquence $\nu$ le libre parcours moyen d'absorption $\lambda_{a,\nu}$ est tel que $\frac{1}{\lambda_{a,\nu}}=\frac{s\gamma}{\pi((\nu-\nu_c)^2 + \gamma^2)}$. Cela correspond à l'absorption d'une raie de Lorentz d'intensité $s$, centrée sur la fréquence $\nu_c$ et de demi-largeur à mi-hauteur $\gamma$. On doit observer que lorsque $\gamma$ devient petit devant la largeur de l'intervalle de fréquence considéré, alors l'incertitude de calcul devient très élevée. Cela vient du fait que l'absorption moyenne que l'on cherche à évaluer correspond aux rares photons qui sont partis avec une fréquence proche du centre de la raie. Pour les autres, la probabilité d'absorption est très faible. La variance du poids de Monte Carlo est donc élevée.

Programme 5 On montrera que si l'intensité de la raie est faible, ou si la dimension du carré est faible, alors l'absorption à chaque fréquence est proportionnelle $\frac{1}{\lambda_{a,\nu}}$. On en déduira que dans de tels cas, on peut améliorer la convergence en utilisant un échantillonnage par importance dans lequel la fréquence est générée aléatoirement selon une densité de probabilité correspondant à la distribution de Lorentz.

Exemple de solution (programmé en fortran) :

c---------------------------------------------------------------------
c Calcul de la fraction absorbée pour un rayonnement incident
c gris et un spectre d'absorption correspondant à une raie de Lorentz
c en fonction de l'inverse du libre parcours moyen
c de diffusion (k)
c---------------------------------------------------------------------
      PROGRAM prog3
      IMPLICIT NONE
      INTEGER iseed
      COMMON/comsee/iseed
      DOUBLE PRECISION pi
      PARAMETER(pi=3.141592654)
c---------------------------------------------------------------------
      INTEGER itir,ntir
      DOUBLE PRECISION w,som_w,som_w2,moy_w,moy_w2,sig_w,sig_moy_w
      DOUBLE PRECISION cote,lambda
      DOUBLE PRECISION x,y,theta,L
      DOUBLE PRECISION r,xold,yold,Lold,d,dsecx,dsecy
      DOUBLE PRECISION ka,k,k0,dk
      INTEGER ik,nk
      DOUBLE PRECISION frac_abs,sig_frac_abs
      DOUBLE PRECISION nu_x,nu_y,nu_c,gamma,ka_max,s,nu,px,py
c---------------------------------------------------------------------
      OPEN(10,FILE='sorties.out')
      PRINT *,'germe du generateur aleatoire : '
      READ *,iseed
c---------------------------------------------------------------------

      nu_x=0.
      nu_y=2.
      nu_c=1.
      gamma=0.0001
      ka_max=0.1
      cote=0.3
      ka_max=0.001/cote
      s=pi*gamma*ka_max
      nk=5
      k0=0.
      dk=1./cote
      ntir=10000

      DO ik=1,nk
         k=k0+ik*dk
         lambda=1./k

         som_w=0.
         som_w2=0.
         DO itir=1,ntir

 2          CONTINUE
            CALL rand_lorentz(nu_c,gamma,nu)
            IF ((nu.LE.nu_x).OR.(nu.GE.nu_y)) GOTO 2
            px=1./(nu_y-nu_x)
            py=gamma/pi/((nu-nu_c)**2+gamma**2)/
     &         ((atan((nu_y-nu_c)/gamma)-atan((nu_x-nu_c)/gamma))/pi)
            ka=s*gamma/pi/((nu-nu_c)**2+gamma**2)

            L=0.

            x=0.
            CALL rand_uniforme(r)
            y=r*cote
            CALL rand_uniforme(r)
            theta=asin(2.*r-1.)

 1          CONTINUE
            
            xold=x
            yold=y
            Lold=L
         
            CALL rand_uniforme(r)
            d=-lambda*log(1-r)
            x=x+d*cos(theta)
            y=y+d*sin(theta)
            L=L+d

            IF ((x.GE.0).AND.(x.LE.cote)
     &           .AND.(y.GE.0).AND.(y.LE.cote)) THEN
               CALL rand_uniforme(r)
               theta=r*2*pi
               GOTO 1
            ELSE
               IF (cos(theta).GE.0.) THEN
                  dsecx=(cote-xold)/cos(theta)
               ELSE
                  dsecx=(0.-xold)/cos(theta)
               ENDIF
               IF (sin(theta).GE.0.) THEN
                  dsecy=(cote-yold)/sin(theta)
               ELSE
                  dsecy=(0.-yold)/sin(theta)
               ENDIF
               IF (dsecx.LE.dsecy) THEN
                  d=dsecx
               ELSE
                  d=dsecy
               ENDIF
               x=xold+d*cos(theta)
               y=yold+d*sin(theta)
               L=Lold+d
            ENDIF

            w=(1.-exp(-ka*L))*px/py
            
            som_w=som_w+w
            som_w2=som_w2+w**2
         ENDDO
         moy_w=som_w/ntir
         moy_w2=som_w2/ntir
         sig_w=sqrt(moy_w2-moy_w**2)
         sig_moy_w=sig_w/sqrt(dble(ntir))

         frac_abs=moy_w
         sig_frac_abs=sig_moy_w
         WRITE(10,*) k,frac_abs,sig_frac_abs

      ENDDO

c---------------------------------------------------------------------
      CLOSE(10)
      STOP
      END
c---------------------------------------------------------------------

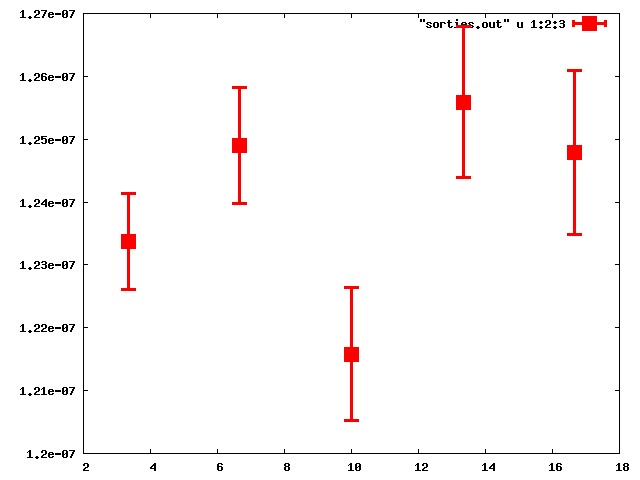
Exemple d'extension en géométrie tridimensionnelle (sous EDStar) : en cours.